环形链表

此题解题思路分为两部分

1. 判断链表中是否有环

可以使用快慢指针法，slow 每次往前走一格，fast 每次往前走两格。这样每次 fast 会比 slow 多走一格，相当于往前去追 slow ，若存在环，则 slow 和 fast 一定会相遇，定义其相遇的节点为相遇节点 index1。

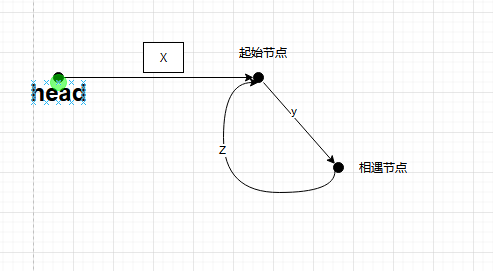
可设距离如下图所示，则 slow 走过的距离为 $x+y$ , fast 走过的距离为 $x+y+n(y+z)$，而 fast 走过的距离应该是为 slow 的两倍，所以有 $2*(x+y) = x+y+n(y+z)$

最后可得 $$x+y = n(y+z)$$

要寻找的节点是起始节点，也就是要寻找 $x$ 的值，化简上述式子可得 $$x = (n-1)(y+z)+z$$

当 $n=1$ 时，有 $x = z$，由此可得，我们寻找环起始节点的方法。

判断链表存在环后，需要寻找环的起始节点。此处也是使用双指针法，一个从相遇节点处开始往前移动，一个从head处往前移动，这样到最后两指针相遇位置就会是环的起始节点